ESTATICA

UNIDAD 1

VECTOR:
Son expresiones matematicas que poseen magnitud, direccion y sentido, los cuales se suman deacuerdo a la ley del paralelogramo.

LEY DEL PARALELOGRAMO:
Establece que dos fuerzas que actuan sobre una particula pueden ser sustituidas por una sola fuerza llamada resultante, que se obtiene al trazar la diagonal del paralelogramo que tien los lados iguales a las fuerzas dadas.

RESULTANTE DE DOS VECTORES.

SOLUCION TRIGONOMETRICA

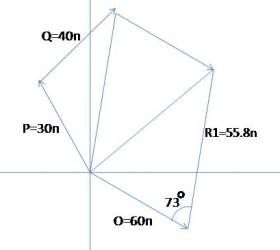
Dos vectores Q y P. Q de 60n y P de 40n.

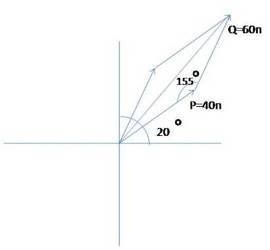
LEY DE COSENOS.

$a=\sqrt{b^2 + c^2 -2bc Cos0}$

$R=\sqrt{40^2 + 60^2 -2(40)(60) Cos155}$

$R=\sqrt{9550.27}$

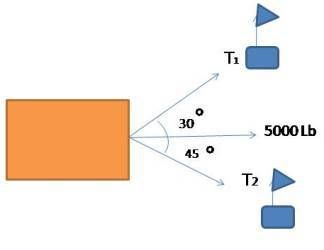
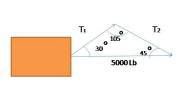
EJEMPLO 2

DETERMINAR LA TENCION EN CADA CUERDA

$\frac{5000}{Sen 105}=\frac{T1}{Sen 45}$

$T1=\frac{(Sen 45)5000}{Sen 105}= 3660 Lb$

$\frac{5000}{Sen 105}=\frac{T2}{Sen 30}$

$T2=\frac{5000(Sen 30)}{Sen 105}=2588 Lb$

FUERZAS CONCURRENTES

Encontrar la resultante
metodo trigonometrico

EJEMPLO
componentes
P= 30n
Q=40n
O=60n

$R= \sqrt{3121}= 55.86$

$\frac{sen B}{40}= \frac{sen 105}{56}$

$sen B=\frac{40 sen 1o5}{56}= 43.62^0$

$R=\sqrt{4760.47}= 69n$

COMPONENTES RECTANGULARES DE UN VECTOR

la fuerza F se descompone en Fx a lo largo del eje X y una componente Fy a lo largo del eje Y. El paralelogramo trazado para obtener las dos componentes es un rectangulo, y las fuerzas Fx y Fy se llaman componentes rectangulares.

Fx= FxI . Fy= FyJ
F= FxI + FyJ

Fx= F cos $\theta$
Fy= F sen $\theta$

$F= \sqrt{F_x^2 + F_y^2}$

$tan \theta = \frac{Fy}{Fx}$

$\theta = Tan^-^1 \frac{Ry}{Rx}$

$\theta$ Es una angulo que forma el vector en el lado positivo del eje de las X´s.

$\left |{R}\right | = \sqrt{Rx^2 + Ry^2}$

$\overrightarrow{R} = Rxi + Ryj$

EJEMPLO

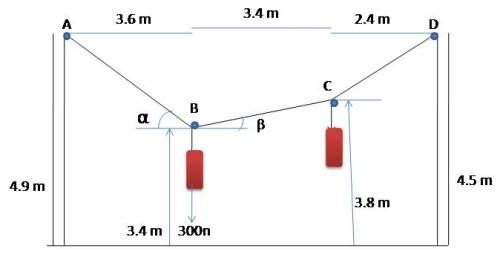
Un hombre jala una cuerda atada aun edificio con una fuerza de 300n. Cuales son las componentes orizontales y verticales de las fuerzas ejercidas en el punto A ?

$\theta = tan^-^1 (\frac{6}{8}) = 36.86^0$

EJEMPLO 2

$R= \Sigma F= 199.29 i + 14.29j$

$\left |{\bar{R}}\right | = \sqrt{(199.29)^2 + (14.30)^2}$

$\theta = tan^-^1(\frac{14.30}{199.29}) = 4.1^0$

EQUILIBRIO DE LA PARTICULA

Una particula se encuentra en equilibrio cuando las fuerzas que actuan sobre ellas satisfacen

$\Sigma F= 0$

EJEMPLO

$\alpha = tan^-^1 (\frac{1.5}{22.61}) = 22.60^0$

$\beta = tan^-^1 (\frac{0.4}{3.4}) = 6.70^0$

$\frac{TBA}{sen 83.3^0}=\frac{TBC}{sen 67.3^0}=\frac{300 n}{sen 29.31}$

$TBC = \frac{300 sen67.3^0}{sen 29.31^0} = 565.35 n$

$TBA = \frac{300 sen83.3^0}{sen 29.31^0} = 608.14 n$

$\beta = tan^-^1 (\frac{0.7}{2.4})= 16.26^0$

$\alpha = 83^0$

$\frac{TBC}{sen 73,74^0}= \frac{TCD}{sen 96.7^0}= \frac{?}{sen9.56^0}$

$\frac{565.35}{sen 73,74^0}= \frac{TCD}{sen 96.7^0}= \frac{?}{sen9.56^0}$

$? = \frac{565.35sen 9.65^0}{sen 73.74^0}= 97.80n$

FUERZAS EN EL ESPACIO

$\overrightarrow{F}=F_X i +F_Y j +F_Z K$

$F = \left |{F}\right |= \sqrt{Fx ^2 + Fy ^2 + FZ ^2}$

$Fx = F cos \theta x$

$Fy = F cos \theta y$

$Fz = F cos \theta z$

$\overline{F}= F (cos \theta _x i +cos \theta _y j + cos \theta _z k)$

$\overline{F}= F \lambda$

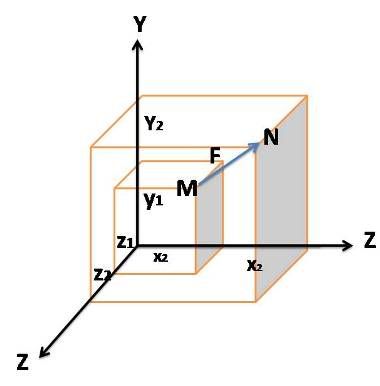
EJEMPLO
¿Determinar la magnitud y direccion de la resultante de las fuerzas ejercidas por el cable AB y AC? AB = 840 Lb AC= 1200 Lb

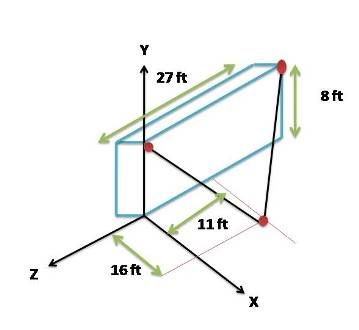
definir segmento

" alt="\vec{AB}= <(0-16),(8-0),(0+11)>" align="absmiddle" width="301" height="24">

" alt="\vec{AC}= <(0-16),(8-0),(-27+11)>" align="absmiddle" width="325" height="24">

$\vec{AB}= -16 \hat{i}+ 8 \hat{j}+11 \hat{k}$

$\vec{AC}= -16 \hat{i}+ 8 \hat{j}-16 \hat{k}$

$\bar{TAB}= TAB. \lambda. AB$

$\lambda AB = \frac{\bar{AB}}{\left |{AB}\right |}= \frac{-16\hat{i}+8\hat{j}+11\hat{k}}{\sqrt{-16^2+8^2+11^2}}$ $=\frac{-16\hat{i} +8 \hat{j}+11 \hat{k}}{21}$

$\bar{TAB}= TAB \lambda AB = 840(-0.76\hat{i} +0.38\hat{j} +0.52\hat{k})$

$\bar{TAB}= -638\hat{i} +319\hat{j} +436\hat{k}$

$\lambda AC = \frac{\bar{AC}}{\left |{AC}\right |}= \frac{-16\hat{i}+8\hat{j}-16\hat{k}}{\sqrt{-16^2+8^2-16^2}}$ $=\frac{-16\hat{i} +8 \hat{j}-16 \hat{k}}{24}$

$\bar{TAC}= TAC \lambda AC = 1200( -0.76\hat{i} +0.38\hat{j} -0.76\hat{k})$

$\bar{TAC}= -792\hat{i} +396\hat{j} -792\hat{k}$

$\bar{R} = \bar{TAB}+\bar{TAC}$

$\bar{R}=(-638-792)\hat{i} +(319+396)\hat{j} +(436-792)\hat{k}$

$\bar{R}=-1430\hat{i} +715\hat{j} -356\hat{k}$

$\theta x = cos^-^1(\frac{Fx}{\left |{F}\right |})$

$\left |{R}\right | = \sqrt{-1430^2+ 715^2 -356^2} = 1638 Lb.$

$\theta x = cos^-^1 (\frac{-1430}{1638})= 150.8^0$

$\theta y = cos^-^1 (\frac{715}{1638})= 64.11^0$

$\theta z = cos^-^1 (\frac{-356}{1638})= 102.55^0$

EQULIBRIO DE UNA FUERZA EN EL ESPACIO

lAas componentes Rx Ry Rz de la resultante estan dadas por las relaciones, al expresar que las componentes de la resultante son cero, se escriben

$\sum_ {} F_x = 0$ $\sum_ {} F_y = 0$ $\sum_ {} F_z = 0$

CUERPOS RIGIDOS:
SISTEMAS EQUIVALENTES DE FUERZAS

FUERZAS ETERNAS E INTERNAS:

Las fuerzas externas representan la accion que ejercen otros cuerpos sobre el cuerpo rigido en consideracion. Ellas son las responsables del comportamiento externo del cuerpo rigido.

las fuerza externas causan que el cuerpo se mueva o aseguran que este permanezca en reposo.

Las fuerzas internas son aquellas que mantienes unidas las particulas que conforman al cuerpo rigido.si este esta constituido en su estructura por varias partes, las fuerzas que mantienen unidas dichas partes tambien se definen como fuerza internas.

PRODUCTO VECTORIAL

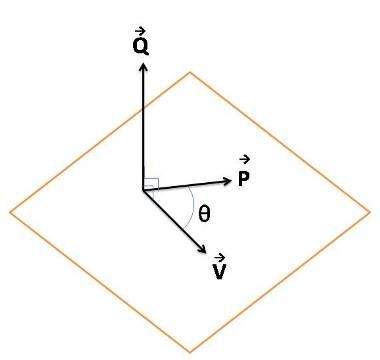
Sean P y V vectores en el mismo plano que forman un angulo $\theta$ entre ellos.

Q perpendicular al plano que contiene a P y V, la magnitud de Q en el producto vectorial de P y V multiplicado por el seno del angulo entre ellos ( $\theta$ )

$\bar{P}* \bar{V}=\bar{P}\bar{V} sen \theta$

La direccion de Q se optiene a partir de la regla de la mano derecha.

PRODUCTO VECTORIAL EXPRESADO EN TERMINOS DE COMPONENTES RECTANGULARES.

i * i = 0 i * j = k i * k = - j

$v= \begin{bmatrix}{i}&{j}&{k}\\{P_x}&{P_y}&{P_z}\\{Q_x}&{Q_y}&{Q_z}\end{bmatrix}$

MOMENTO DE UNA FUERZA CON RESPECTO A UN PUNTO

El momento de F con respecto a O se define como el producto vectorial de r * F

$M_o = rF sen \theta = Fd$

TEOREMA DE VARIGNON

componentes rectangulares del momento de una fuerza

M = yF_z - zF_y M = zF_x - xF_z M = xF_y - yF_x

EJERCICIO
¿DETERMINAR EL MOMENTO CON CON RESPECTO AL PUNTO A DE LA FUERZA EJERCIDA POR EL ALAMBRE EN EL PUNTO C ? tencion en el alambre es de 200 N

$\bar{M_A}= \bar{r} * F$

$\bar{M_A}= \bar{r_A_C} * \bar{T} _C_D$

$\bar{T}_C_D = TCD \lambda C D$

$\frac{\bar{CD}}{\left |{CD}\right |} = \frac{(-0.3 + 0.24 .032)}{\sqrt{-0.3^2+ 0.24^2 +0.32^2}}$

$\bar{T}_C_D = -120\hat{i} +69\hat{j}-128\hat{k}$

$\bar{r}_A_C = 0.3\hat{i}+0\hat{j}0.8\hat{k}$

$M_A =\begin{bmatrix}{\hat{i}}&{\hat{j}}&{\hat{k}}\\{0.3}&{0}&{0.08}\\{-120}&{96}&{-128}\end{bmatrix}$

$= \hat{i}[(0*-128)-(96)0.08] - \hat{j}[(0.3*-128)-(-120*0.08)] \hat{k}[(0.3*96)-(-120*0)]$

$= -7.68 \hat{i} +28.8 \hat{j} +28.8 \hat{k}$

MOMENTO PAR

Se dice que dos fuerzas F y -F que tienen la misma magnitud, lineas de accion paralelas y sentidos opuestos forman un par.
La suma de los momentos de las dos fuerzas con respecto a un punto dado no es cero.

Aun que las dos fuerzas no originaran una traslacion del cuerpo sobre el que esta actuando, estas si tenderan a hacerlo rotar.

ANALISIS DE ESTRUCTURAS

ARMADURAS

las ermaduras es uno de los principales tipos de estructuras que se usan en la ingenieria. Esta proporciona una sola solucion practica y economica para muchas situaciones de ingenieria, en especial par el diseño puentes y edificio.

ANALISIS DE ARMADURAS MEDIANTE EL METODO DE LOS NODOS.

En una armadura se puede desarmar y dibujarse un dagrama de cuerpo libre para cada perno y cada elemento. Cada elemneto esta sometido a la accion de dos fuerzas, una en cada uno de sus extremos, estas fuerzas tienen la misma magnitud, la misma linea de accion y sentidos opuestos.

la tercera ley de newton indica que ñlas fuerzas de accion y reaccion entre un perno y un elemento son iguales y opuestas. por tanto la fuerza ejercida por un elemento sobre lso dos pernos a los cueles se conecta deben de estar dirigidos a lo largo de ese elemento y debe ser igual y opuesto

Como la armadura en su totalidad esta en quilibrio, cada perno debe estar en equilibrio. en el que unperno este en quilibrio se expresa debujando su diagrama de cuerpo libre y escribiendo dos ecuaciones de equilibrio. por tanto, si una armadura tiene n pernos, habra 2n pernos ecuaciones dispoibles, las cuales podran resolverse para 2n incognitas.

EJEMPLO

UTILIZAR EL METODO DE NODOS PARA DETERMINAR LA FUERZA PRESENTE EN CADA ELEMENTO DE LAS ARMADURA Y ESTABLESER SI LOS ELEMENTOS ESTAN EN TENSION O COMPRESION.

$\sum F_X = 0 \frac{1}{\sqrt{2}}F_A_B - \frac{4}{5}F_B_C = 0$

$\sum F_Y = 0 \frac{1}{\sqrt{2}}F_A_B + \frac{3}{5}F_B_C -4.2 KN = 0$

$\frac{7}{5}F_B_C = 4.2KN$ ...............

$F_A_B = \frac{12\sqrt{2}}{5}KN$ ....................

$\sum FX= 0 : \frac{4}{3}3.00 KN - \frac{12}{13}F_A_C= 0$

$F_A_C= \frac{13}{5}KN$ .........

ANALISIS DE ARMADURAS MEDIANTE EL METODO DE SECCIONES

El metodo de los nodos es el mas eficiente cuando se deben determinar las fuerzas en todos los elementos de una armadura.

si solo se desea encontrar la fuerza en un elemento o en un numero muy reducido de elementos, el metodo de secciones es el mas eficiente.

EJEMPLO

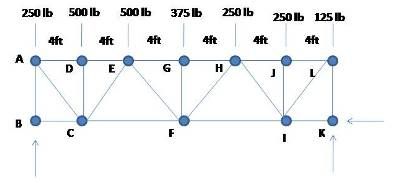
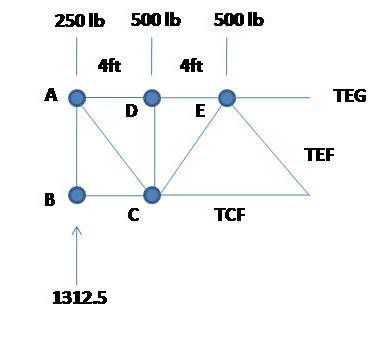
Una armadura para piso se carga en la forma que muestra la fig.
Determine la fuerza presente en los elemnetos CF, EF Y EG.

$\sum F _X = 0$

$\sum M_X = 0 : 6 * 4((K_Y-125LB)-5*4(250LB)) - 4*4((250LB))-3*4((375))-2*4((500LB))-4((500LB))=0$

$\sum F_Y =0 : A_Y -3(250)-2(500)-375+125+937.5=0$

$\sum M_E =0 : (2)F_C_F+(4)(500) +(8)(250-1312.5)= 0$

$\sum F_Y= 0 1312.5-250-2(500)-\frac{1}{\sqrt{5}} F_E_F=0$

$\sum F_X= 0 3250+\frac{2}{\sqrt{5}}( 62.5\sqrt{5})-F_E_G=0$

CENTROIDES.

Hasta ahora de ha supuesto que la atraccion ejercida por la tierra sobre un cuerpo rigido podria representarse por una sola fuerza W.
Esta fuerza denominada fuerz de gravedad o peso de cuerpo , debia aplicarse en el centro de gravedad del cuerpo, de hecho, la tierra ejerce una fuerza sobre cada una de las particula que constituyen al cuerpo, En este sentido la accion de la tierra sobre un cuerpo rigido debe representarse por un gran numero de pequeñas fuerzas dsitribuidas sobre todo el cuerpo. la totaluidad de dichas fueras pequeñas pueden ser reemplazada por una sola fuerza qeuivalente W

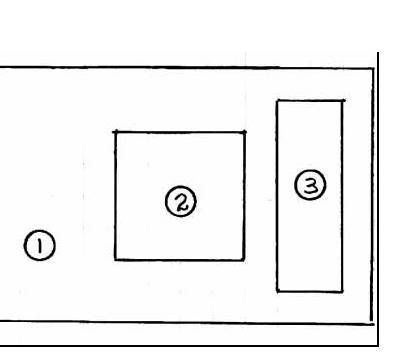
EJEMPLO

LOCALIZAR EL CENTROIDE DEL AREA PLANA MOSTRADO EN LA FIGURA.

$\bar{X}= \frac{\sum \bar{X}A}{\sum A}}= \frac{21000000}{150000} = 140$

$\bar{Y}= \frac{\sum \bar{Y}A}{\sum A}}= \frac{24750000}{150000} = 165$

MOMENTOS DE INERCIA

TEOREMA DE LOS EJES PARALELOS O TEOREMA DE STEINER

Considere el momento de inercia I de un area A con respecto a un eje AA´ si se representa con y la distancia desde un elemento de area dA hasta AA´. se escribe:

FORMULA

$I = \int y^2 dA$

Esta formula expresa el momento de inercia I de un area con respecto a cualquier eje dado AA´ es igual al momento de inercia I del area con respecto a un eje centroidal BB´que es paralelo a AA´ mas el producto del area A y el cuadrado de la distancia d entre los dos ejes.

este teorema se conoce como el teorema de los ejes paralelos o teorema de steiner.

MOMENTOS DE INERCIA DE AREAS COMPUESTAS

Unarea compuesta A que esta constituida por varias areas componentes A1,A2,A3,... Como la integral que representa el momento de inercia de A puede subdividirse en integrales evaluadas sobre A1,A2,A3,..... el momento de inercia de A con respecto a un eje dado se obtiene sumando los momentos del area A1,A2,A3,... con respecto al mismo eje.

EJEMPLO

PARA EL AREA SOMBREAA DETERMINAR EL MOMENTO DE INERCIA Y L RADIO DE GIRO CON RESPECTO AL EJE X.

$[\frac{1}{12}(12)(8)^3 ]-[\frac{1}{12}(5)(4)^3 ]-[\frac{1}{12}(2)(6)^3 ] in^2 = 449.33 in^4$

$K_X = \sqrt{\frac{449.33}{64}} = 2.65$

ESTATICA

jueves, 5 de marzo de 2009

ESTATICA

Seguidores

Archivo del blog

Datos personales